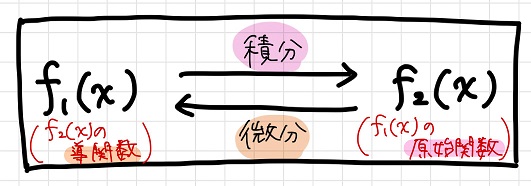
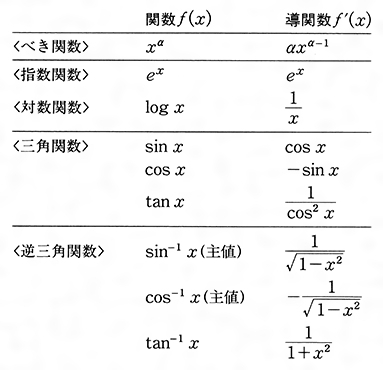
ライプニッツとニュートン:微積分学発見の優先権論争 ライプニッツはデカルトやパスカルと同様、数学や自然科学の分野においても顕著な業績を残した。 とりわけ数学の分野においては、微分積分学と記号論理学の創始者として、歴史的な業績を上げた。 ライプニッツが微分法の研究に打ち込んだのは、パリに滞在していた1675年から76年にかけてであるが、彼が ゴットフリート・ライプニッツにより採用されたライプニッツの記法は数学分野で広く使用されている。この記法は特に関数 y = f(x) が従属変数 y と独立変数 x の関数関係を表すものとみるときに用いられる。 この場合、導関数は のように書かれ( d はこのように立体にする流儀とイタニュートン、ライプニッツによる微分積分法の創始 イギリスのニュートンは、f(x,y)をx、yの多項式としてf(x,y)=0という曲線上を動く点を考えた。そして、この点の水平方向の速さ、垂直方向の速さをそれぞれ 、 で表し、これらをx、yの流率とよんだ。 この流率の比 / は接線の傾きであり
ネイピア数とは 自然対数の底eについて解説 空間情報クラブ 株式会社インフォマティクス
微分 ニュートン ライプニッツ
微分 ニュートン ライプニッツ-7 ニュートンとライプニッツ(先取権論争について) 71 先取権論争とは ライプニッツ(1646−1716)は,パリ滞在期(1672−76)に無限小解析(=微分積分学) の基本となる,記号法,計算のアルゴリズムを確立した.接線問題や求積問題において,導関数(微分)はニュートンとライプニッツが別々に考え出したと言われ,導関数を表わす記号も,ニュートンの記号 y', f'(x) と,ライプニッツの記号 ,




微積分にひそむ エニグマ の正体を探る 古本買取のエコブックス スピード査定で宅配買取 大阪まで送料無料で古本買取
しかし、微積分の教科書でニュートンの名を目にする事は殆どない。 今や微積分の関数で目にする記号は、その殆どがライプニッツが記述したものである。 事実、ニュートンが確立した微積分は、結果的にはライプニッツと殆ど同じにもかかわらず、評価されたのは英国内に留まった。 一方、ライプニッツの微積分は当時から広くヨーロッパの数学者に採用されライプニッツの無限小概念 律に基づき無限小を用いる方法を提示した(Bos, 1974)。(3) は、アルキメデスの取り尽し 法(1) をより一般化したもので、無限小を用いない。(4) の連続律は(1) でなされる極限移 行を保証するための原理であり、その証明はBos (1974, x44) で再構成されている。1 微分法と運動方程式 11 ライプニッツと微分法 ライプニッツの生涯 ゴットフリート・ヴィルヘルム・ライプニッツ(Gottfried Wilhelm Leibniz, )は,ドイツ(神聖ローマ帝国)のライプツィヒ出身の哲学者,数学者,科学者であり,幅広い分 野で活躍した学者・思想家として知られている。
通常ニュートン, ライプニッツ が微分積分学の 「創始者」 と目されるのは, それらの 「デカルトを越えた」 点にあるからである 技法として無限級数を利用する場面, さらには独自の記号法の開発もデカルトの残した課題解決 の中で見ることができる本書は,この現代人の必修科目ともいうべき微分・積分を総特集したNewton別冊『微分と積分 新装版』の改訂版です。 知識ゼロからでも楽しく読み進めていただけるよう,微分・積分のエッセンスをやさしく解説した特集記事を新たに収録しました。 このほかにも,微分・積分を誕生させた時代背景や数学者たちの思考,微分・積分の計算問題や応用事例なども収録ニュートンとライプニッツ 歴史的に言いますと、微分積分を見つけたのはニュートンとライプニッツ (1646~1716)だと言われています。 ニュートンとライプニッツは17世紀中ごろに生まれて、18世紀初頭に亡くなっています。 微分積分はこの時代に作られたのです。 ニュートンとライプニッツはどちらが最初に微分積分を発見したのか、大論争をしています。 それは
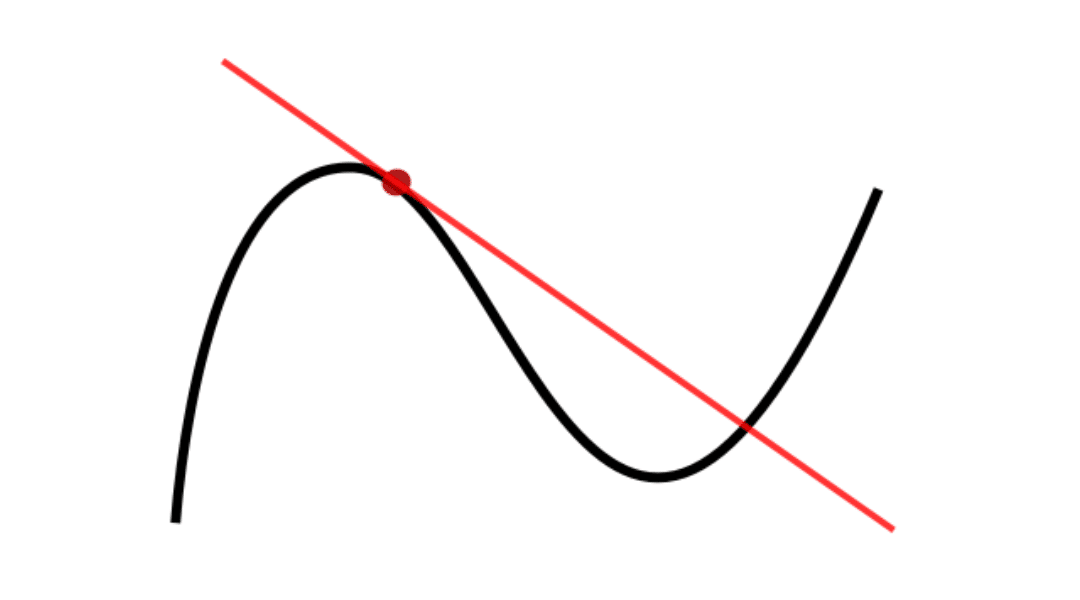
N=1 n = 1 の場合の「積の微分公式」は既知とする。 証明は →積の微分公式とその証明の味わい n = t n=t n = t のときライプニッツの公式が成立すると仮定して t 1 t1 t 1 階微分を計算していく。 まず,帰納法の仮定より ( f g) ( t 1) = ( ∑ k = 0 t t C k f ( k) gライプニッツ、ニュートン、 渡邉俊夫 ライプニッツの公式 積の 𝑛𝑛 階微分を求める式 ライプニッツの公式②微分係数と接線の方程式 f(x) のx0 での微分係数の定義は次の様に書き変えられる: lim x→x0 f(x)−f(x0) x−x0 −f′(x 0) = 0 つまり とおくと このことは を の近くで一次関数 で近似すると、 が に近付くとき「余り」 は の 一次式より速く に近付くということである。



2




微分積分学 Wikipedia
ニュートンと泥仕合、追いつけない天才 1702年の肖像画 – 参照:Wikipedia ニュートンとの対立 1695年になって、ニュートンは微分・積分の功績がライプニッツのものという見方になっているのを知りました。ライプニッツとニュートン:微積分学発⾒の優先権論争 ライプニッツが微分法の研究に打ち込んだのは、パリに滞在していた1675年から76年に かけてである。 ライプニッツよりも10年ほど前に、ニュートンが⼒学的な観点から微分法を発⾒していた。ニュートンとは別に、異なった視点から微積分法を確立した数学者がいました。 それがゴットフリート・ライプニッツ(Gottfried Wilhelm Leibniz )です。




微分積分学の史的展開 ライプニッツから高木貞治まで 高瀬 正仁 講談社book倶楽部



微分積分 微分と積分との間のふか い関係とは 微分と積分の統一による革命 黒豆納豆の特許翻訳
ニュートン記法の微分記号 微分記号の記法としては といったライプニッツの記法が一般的です。しかし力学系等の分野によっては のようなニュートンの記法の方が好まれる場合もあります。ゆっくり解説数学史一番の論争 ニュートンVSライプニッツ微分積分 解説・講座 初投稿です。知りたい!サイエンス 1 ニュートンとライプニッツは、ともに17世紀から18世紀にかけて微分積分を作り出した天才です。どちらが先に作り出したのか言い争ったというのは有名なエピソードです。そんな二人が考えた微分積分とはどんなものなのでしょうか。




はじめての解析学 微分 積分から量子力学まで 原岡 喜重 ブルーバックス 講談社book倶楽部




微分積分学の史的展開 ライプニッツから高木貞治まで 高瀬正仁 とね日記
微分積分学の誕生、厳密化と発展 ニュートン, ライプニッツ 微分積分学の創始。無限小・無限大の概念、 微分積分学の基本定理など ニュートン(1642~1727 年) とライプニッツ(1646~1716 年)微分積分学に対する アイザック・ニュートン と ゴットフリート・ライプニッツ のアプローチは17世紀にさかのぼる。 19世紀には数学者たちは微分と積分に対してライプニッツの記法を表現上のものとして採用したことにより決着した。D 時空 ニュートン ライプニッツ e 量子力学 アインシュタイン ボーア ニュートンは実在的世界記述法の中心人物なのだから, (必要悪のような, または人為的なよう な) 座標に基づく微分方程式を使いたくなかったと思いたい ニュートンにとっては,



ライプニッツの公式 具体例と証明 理数アラカルト




ライプニッツの記法 Wikipedia
吉田 信夫『ニュートンとライプニッツの微分積分 ~離散と連続から考える~』の感想・レビュー一覧です。ネタバレを含む感想・レビューは、ネタバレフィルターがあるので安心。読書メーターに投稿された約2件 の感想・レビューで本の評判を確認、読書記録を管理することもできます。数学は苦手? 微分積分はむずかしい? 微分積分の生みの親アイザック・ニュートンはどのような思考を経て微分積分を生みだしたのでしょうか。彼の頭の中をのぞきながら,「微分積分」のきほんを楽しく身につけてみませんか? isbn




楽天市場 ニュートン 微分 積分の通販




ニュートンの知られざるダークサイド2 闘争編 アザミン Note




ライプニッツとニュートン なぜ差がついたか それは 記号 だ 佐藤 恒雄 ブルーバックス 講談社 1 2




微分積分を速度と距離の関係で理解する 自然科学研究会2 生活の中の数学 その2



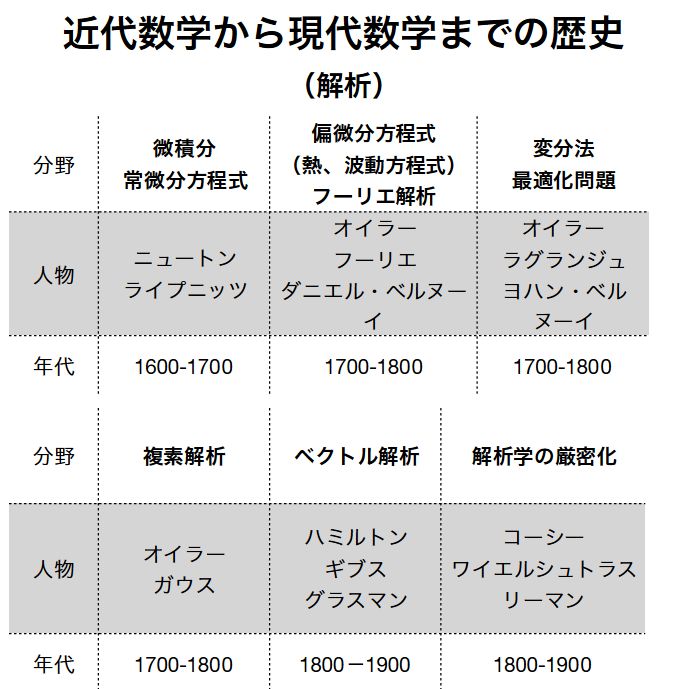
数学の歴史



2




ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する




マニラ68歳男の生涯学習 微分積分 Munetomo Club 棟朝淳州




分数階微積分とは何ですか




ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する




科学雑誌newton ニュートン 公式 別冊 微分と積分 新装版 発売 微分 積分は 飛行機や建築物などの設計 株価の変化など さまざまな場面で欠くことのできない数学の手法です 6 18発売のnewton別冊 微分と積分 新装版 は 創始者ニュートンの
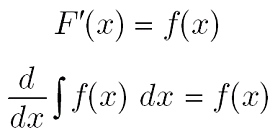



積分 微積分学の 基本定理 大人が学び直す数学



Http Www Kurims Kyoto U Ac Jp Kyodo Kokyuroku Contents Pdf 1677 17 Pdf



微分法とは コトバンク



微分積分法を活用する力を養う入門書 ちくま学芸文庫 俣野 博 Webちくま



2



微積分が導いた宇宙の法則 万有引力の発見は数学の賜物 サイエンス テクノロジー 研究 社会連携 京都産業大学




ゆな בטוויטר ニュートンとライプニッツによる微積分学よ発見をめぐる争い ニュートン ライプニッツ 数学史 微分 積分




微分積分学の基本定理のパワーポイントがダウンロードできるようにしました 中学数学 高校数学のサイト ときどき大学数学



自然界を書き表す記号 Sign 微分の世界 佐古昭博 Note




おはアヤ 今日はライプニッツが初めて積分記号 Sを縦長にした感じのアレ を用いてちょうど345年めの記念日です 微分積分は 人類の偉大な発明の一つです ライプニッツとニュートンがほぼ同時期に そ コペルくんwithアヤ先生 Note大学初代教授 Note




ゆっくり茶番 数学の歴史 ニュートンとライプニッツが喧嘩 微分積分学について Youtube




朝日おとなの学びなおし 数学 感動する 微分 積分 By 桜井進




山本貴光 V Twitter Newton 18年11月号 ニュートンプレス も微分積分特集 ニュートン ライプニッツ その他 世界を変えた書物 展に本が出ていたみなさんもご登場




ニュートンとライプニッツの微分積分 離散と連続から考える 知りたい サイエンス 1 アップ研伸館 編集 吉田信夫 著 古本 中古本 古書籍の通販は 日本の古本屋 日本の古本屋




微分の表記方法 Dy Dxのdって何 物理のいろは




ゆっくり茶番 数学の歴史 ニュートンとライプニッツが喧嘩 微分積分学について Youtube




ライプニッツとニュートン 限りなき論争の行方 4 13更新 人類史上最も偉大な天才アイザックの偉業 象が転んだ




ゆな בטוויטר ニュートンとライプニッツによる微積分学よ発見をめぐる争い ニュートン ライプニッツ 数学史 微分 積分




微分法とは コトバンク




数学大百科事典 仕事で使う公式 定理 ルール127 Pdf版 Seshop Com 翔泳社の通販




ニュートン デカルト ライプニッツ フェルマー ラッセル アインシュタイン 独言のネット絵師 光る風便り 鉛筆で描く肖像画 寄川靖宏




無限の問題を解消した 極限 ーそれは100年の努力によって生み出されたー Youtube



微分積分学の基本定理 Wikipedia




微分積分学の史的展開 ライプニッツから高木貞治まで 高瀬正仁 とね日記



ライプニッツの公式 具体例と証明 理数アラカルト




ゆっくり茶番 数学の歴史 ニュートンとライプニッツが喧嘩 微分積分学について Youtube




岩波書店 Twitterren 今日はドイツの哲学者 数学者ライプニッツ の誕生日 1946年 モナド論ないし予定調和の説により 哲学上 神学上の対立的見解の調停を試みました また ニュートンとは独立に微分積分学を発見 発展させた功績でも知られています




メルカリ 微分 積分を楽しむ本 ノンフィクション 教養 300 中古や未使用のフリマ




微分の記法 Wikipedia




微分積分法 を発見した学者が実は二人いた リンゴで有名な物理学者 ともう一人は ナゾロジー




ニュートンの大発明微分と積分 これならわかる ニュートンムック Newton別冊サイエンステキストシリーズ 本 通販 Amazon



微分の表記法にはニュートン表記やライプニッツ表示などがありますが 微分の Yahoo 知恵袋



ライプニッツの公式 具体例と証明 理数アラカルト




ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する




微分積分学の誕生 デカルト 幾何学 からオイラー 無限解析序説 まで 高瀬 正仁 本 通販 Amazon



2



厳密さ 証明が現代数学で要求されるのはなぜ 近代数学の歴史をたどる 趣味の大学数学




微分導入時の雑談 怜悧玲瓏 高校数学を天空から俯瞰する




筑摩書房 近世の数学 無限概念をめぐって 原 亨吉 著



ライプニッツの公式 具体例と証明 理数アラカルト




ニュートンの記号を使う 17 怜悧玲瓏 高校数学を天空から俯瞰する



微分積分において ライプニッツの記法ではdyやdxといった表記を用います あなたはこの表記を ローマン体で書きますか それともイタリック体で書きますか Quora




ライプニッツとニュートン なぜ差がついたか それは 記号 だ 佐藤 恒雄 ブルーバックス 講談社 1 2



ネイピア数とは 自然対数の底eについて解説 空間情報クラブ 株式会社インフォマティクス



1



Http Www2 Tsuda Ac Jp Suukeiken Math Suugakushi Sympo12 12 4okamoto Pdf
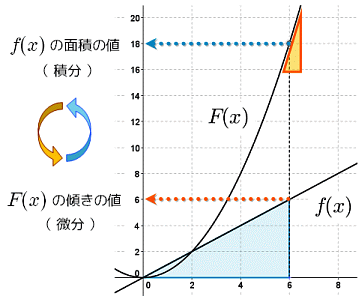



積分 微積分学の 基本定理 大人が学び直す数学




微分と積分 増補改訂版 ニュートンムック 本 通販 Amazon




ライプニッツとニュートン なぜ差がついたか それは 記号 だ 佐藤 恒雄 ブルーバックス 講談社 1 2



微積分 学 と は



微分積分学を発見したのはライプニッツですか それともニュートンですか Yahoo 知恵袋



ニュートンとライプニッツのどちらが微分積分の発祥ですか Quora




ゆっくり茶番 数学の歴史 ニュートンとライプニッツが喧嘩 微分積分学について Youtube



ライプニッツの公式 具体例と証明 理数アラカルト




異なる種類の微積分の探索




お理工さん の微分積分 日本評論社



微分積分とは 高校で習う公式一覧 基本定理や記号の意味も 受験辞典




微分積分学21講 天才たちのアイディアによる教養数学 中村滋 著 本 オンライン書店e Hon




ニュートンとライプニッツの微分積分 離散と連続から考える 知りたい サイエンス 吉田 信夫 本 通販 Amazon




ニュートン デカルト ライプニッツ フェルマー ラッセル アインシュタイン 独言のネット絵師 光る風便り 鉛筆で描く肖像画 寄川靖宏




微分積分学 Wikipedia




Newtonライト 微積のきほん ニュートンプレス




Newtonライト2 0 微分積分 ニュートンプレス
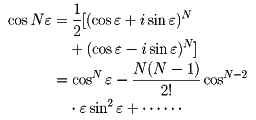



微分積分法とは コトバンク




ニュートンの大発明微分と積分 これならわかる ニュートンムック Newton別冊サイエンステキストシリーズ 本 通販 Amazon




微分と積分 改訂第2版 ニュートンプレス




ゆきさん の ひとりごと 微分の歴史




ゆな בטוויטר ニュートンとライプニッツによる微積分学よ発見をめぐる争い ニュートン ライプニッツ 数学史 微分 積分




目次を見る




Gan S Blog フォーラム



ニュートンの大発見 微分と積分は逆関係 Youtube
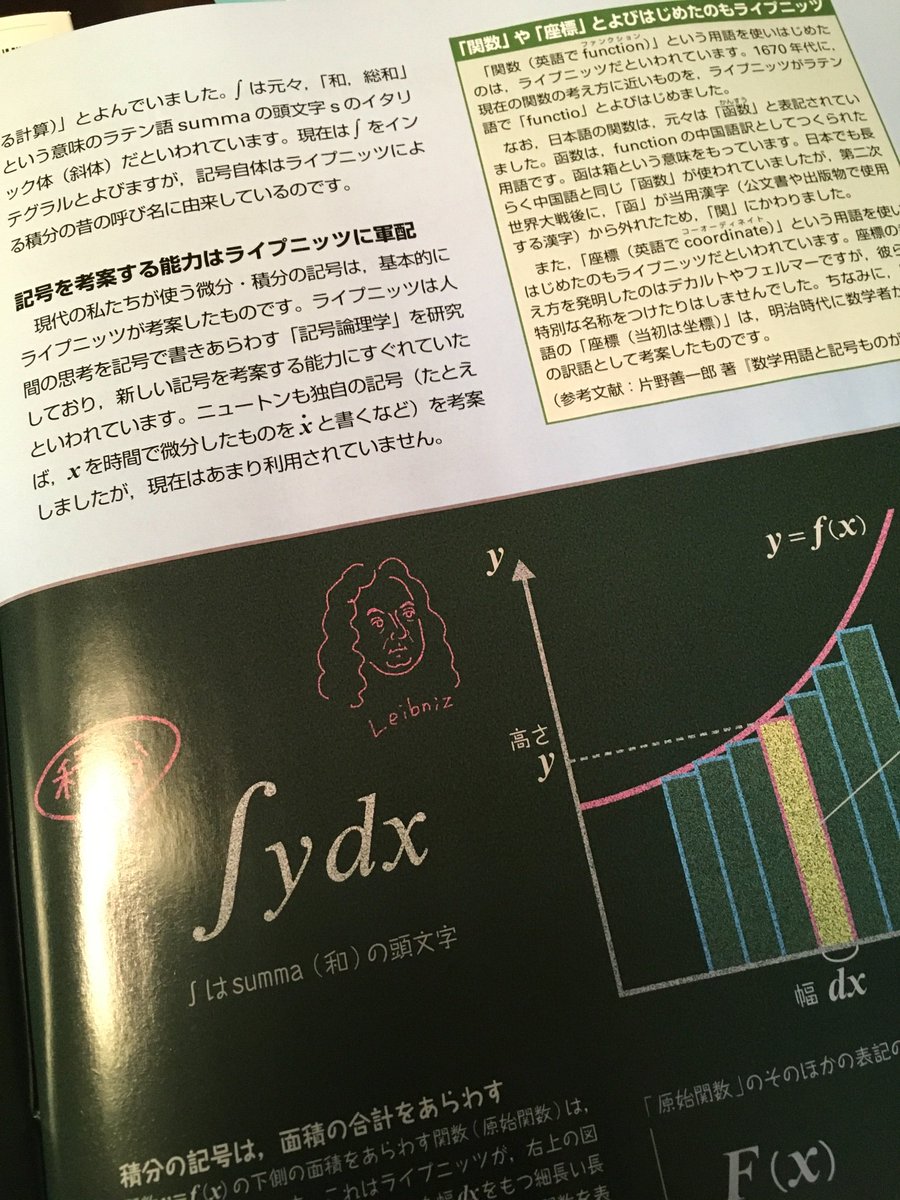



山本貴光 V Twitter Newton 18年11月号 ニュートンプレス も微分積分特集 ニュートン ライプニッツ その他 世界を変えた書物 展に本が出ていたみなさんもご登場




ニュートンとライプニッツの微分積分 離散と連続から考える 知りたい サイエンス 吉田 信夫 本 通販 Amazon



ニュートンとライプニッツのどちらが微分積分の発祥ですか Quora




微積分にひそむ エニグマ の正体を探る 古本買取のエコブックス スピード査定で宅配買取 大阪まで送料無料で古本買取



3



ライプニッツの公式 具体例と証明 理数アラカルト



2



授業での雑談ネタ 怜悧玲瓏 高校数学を天空から俯瞰する



2




37 微積分 数学史 ニュートン ライプニッツ Youtube




文系のためのめっちゃやさしい 微分積分 ニュートンプレス



1




微分 微分の表記 ラグランジュ記法とライプニッツ記法 大人が学び直す数学



Q Tbn And9gcsr Xmdb Fatxio5m2tdsh4opciv9dhglbdbo5hd6c2bqexkb39 Usqp Cau



0 件のコメント:
コメントを投稿